
- #Method of moments estimator for exponential distribution how to#
- #Method of moments estimator for exponential distribution pdf#
Here, the maximum is achieved at an endpoint of the acceptable interval. In Section 4 certain characterizations of GEME. Im trying to find the method of moment estimators for and. Moments, mode, median, information generating function of GEME distribution are discussed in Section 3. A general answer is that an estimator based on a method of moments is not invariant by a bijective. Calculating method of moments estimators for exponential random variables. Find a method of moments estimator for Uniform distribution (theta1, theta2) 0. Method-of-moments estimator for a uniform distribution.
\frac$ cannot be obtained by setting the derivative of the likelihood function to zero. Normal (unknown mean and variance), exponential, and Poisson all have sufficient statistics equal to their moments and have MLEs and MoM estimators the same (not strictly true for things like Poisson where there are multiple MoM estimators). (Location-scale family of exponential distribution) 1. Hence, 1 1 and the method of moment estimator (or m.m.e.) for is D OD1O 1 D1NX.
#Method of moments estimator for exponential distribution pdf#
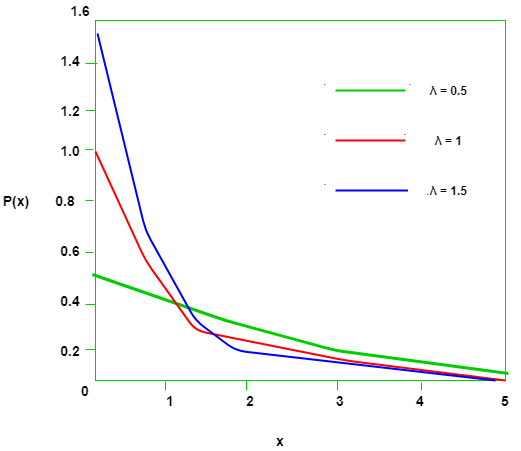
In your case, you have only one parameter $\theta$, so all you need to do is compute the expectation of the distribution you are given, and equate it to the sample mean $\bar X$, and solve the resulting equation for $\theta$.If $X \sim Uniform (0, \theta)$, then the PDF and CDF of $X$ are given by Consider the exponential distribution with parameter.

This is because if you have two unknown parameters, you would need to solve a system of two equations for the two unknowns, and using only the first moment will give only one equation or constraint. Here is an example using an exponential distribution: suppose $X \sim \operatorname^n X_i^2,$$ also known as the second sample moment, respectively. It starts by expressing the population moments (i.e., the expected values of powers of the random variable under consideration) as functions of the parameters of interest. The same principle is used to derive higher moments like skewness and kurtosis.
#Method of moments estimator for exponential distribution how to#
1 E(Y) + 1 Y m1 1 E ( Y) + 1 Y m 1 where m m is the sample moment. We briefly describe different frequentist methods of estimation approaches, namely, maximum likelihood estimators, moments estimators, L-moment estimators. In statistics, the method of moments is a method of estimation of population parameters. How to find estimator for shifted exponential distribution using method of moment I have f,(y) e(y), y, > 0 f, ( y) e ( y ), y, > 0. The method of moments estimator is found by taking the raw moments of the distribution and equating them with the sample moments, until a unique solution is found for the resulting system. How to find estimator for shifted exponential distribution using method of moment I have f,(y) e(y), y, > 0 f, ( y) e ( y ), y, > 0.


 0 kommentar(er)
0 kommentar(er)
